今週はゲームの進捗動画は無いので雑談
今作成しているカジュアル系弾幕ゲームは自機管理の設計中で、動画に撮れるような進捗がないので雑談にします。1年以上前のネタを別方向から見てみました。
以前、外国の科学者さんがスーパーマリオワールドの重力を計算して話題になりました。以下はその動画で、日本語での紹介はEngadgetさんの記事が詳しいです。
まず重力(重力加速度)を求める式は動画の2:40に登場します(下図左)。hはジャンプ高で、tは頂点までの到達時間(rise time)をさしています。この式にゲームで計測した頂点到達時間とマリオの身長を155cmと仮定したジャンプ高を代入(下図右)して重力加速度78m/s2を得ています。これは地球の9.8m/s2の約8倍となるため8Gとなるわけです。
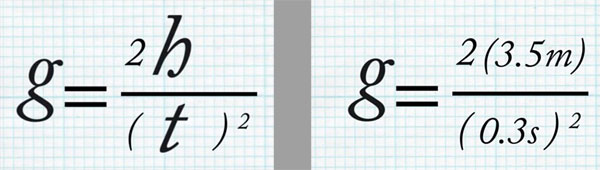
身長155cmで2頭身の人?
この動画の1:57でマリオを155cmの人間と仮定して計算を開始しています。しかし頭身的にマリオを人間と仮定するのは無理があると思うのです。(個人的に)マリオは動く人形としたほうが納得いくので、地球上で稼働する人形と仮定して計算したいと思います。
前述の式に当てはめると、まず地球上なので左辺のgは9.8となります。ゲームから計測しているので頂点への到達時間は0.3秒と変更はありません。なので求めることになるのはジャンプした距離hとなります。つまり「9.8 = 2h / (0.3)^2」を解き、ジャンプ高h=0.441mを得ることができます。
平たく言うと、地球上で0.3秒で頂点に到達するのは約44cmジャンプしたときとなります。動画の2:18でジャンプ高はマリオの2.25倍と説明しているので、ジャンプ高の44cmを2.25で割ればマリオの身長が算出できます。ということでゲームの世界が地球の場合、動いているマリオ人形の身長は約20cmと算出できます。
重いものほど速く落ちる?
記事が短いので重力の話をもう少し。
学校の教科書では「同じ高さから落とすとき重さに関わらず同時に地面に落ちる(空気抵抗を考えない場合)」と習いますが本当でしょうか?
物質はすべて引力を持つ(万有引力)、そして質量が大きいほど引力は高くなります。引力を算出する式はF = G(Mm/R^2)となります。(wikipedia:万有引力)
上記の式は2つの物質間の引力を求めます(変数のMとmは2つの物質の質量を指します)。地球上での引力を求める場合は、Mを地球の質量とするとmは落ちる物質の質量となります。つまり引力は落ちる物質の質量によって変化します。では教科書が間違っているか?というと、そうも言えません。
慣性の法則
慣性とは簡単にいうと「動いている物は動き続けようとし、止まっている物は止まり続けようとする」というものです(wikipedia:運動の第1法則)。
wikipediaでは説明されていませんが、慣性の法則は質量よって変化します。平たく言うと、「重いと動かしにくく、軽いと動かしやすい(無重力下でも)」という感じです。つまり「重い物は引力が大きいけれど同時に動かしにくいため、結局は軽い物と同じ速度で落ちる」ことになります。ということで結局は教科書が正しい感じです。
重力質量と慣性質量
厳密には前述の「2つの質量」は区別されます。最初に説明した引力での質量は「重力質量」と呼ばれ、慣性での質量は「慣性質量」と呼ばれます(wikipedia:二つの質量)。
現在の科学者たちも、2つの質量は同じなのか「ズレがあるのか」調べている最中です(wikipedia:二つの質量の「等価原理」を参照)。現在の測定器の精度で見る限りは「ズレはない」のですが、まだ結論はついていないようです。
→参考:google検索「慣性質量 重力質量 実験」
twitterを本格的に初めてみた。ブログの更新記事をつぶやくのがメイン。あとCocos2dやUnity、その他アプリ開発に関連するツイッターの方をフォローして情報も集められたらなぁと思います。
— 柳澤@ゲーム作るよ (@designdrill) 2015, 12月 28
